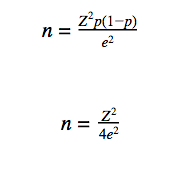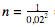Comprenda en esta publicación todo lo que necesita sobre el error de muestreo y el tamaño de la muestra. Aprende a utilizar estos conceptos a tu favor para optimizar tus búsquedas y obtener los mejores resultados utilizando pocos recursos. Véase a continuación:

por Fernando Saraiva

En las elecciones de un país, ¿cuántas personas deben ser entrevistadas para conocer los porcentajes exactos de personas que tienen la intención de votar por cada candidato? Si el objetivo es realmente conocer la información de una manera completamente precisa, la respuesta es simple: es necesario entrevistar a todas las personas del país.

Sin embargo, en un país de dimensiones continentales, como Brasil, entrevistar a todas las personas es completamente inviable. Las cantidades de tiempo y dinero gastadas en investigaciones como esta serían absurdamente grandes. Sin embargo, ¿es realmente necesario conocer los porcentajes exactos de las intenciones de voto de cada candidato? ¿Cuál es la necesidad real? ¿No serían suficientes los resultados aproximados?

Lo cierto es que, sobre todo en investigaciones relacionadas con poblaciones muy grandes, no se analiza a toda la población, sino solo a una parte de ella, llamada muestra. Esta muestra se elige con un tamaño suficiente para que su comportamiento pueda ser una buena aproximación o estimación para el comportamiento de toda la población, es decir, la muestra debe ser representativa de la población.

Obviamente, cuando solo se analiza una parte de la población, y no la totalidad, se obtienen resultados diferentes, debido a que se perdió una parte de la información total, ya que la muestra no contiene todos los elementos de la población. El objetivo es elegir una muestra que represente bien a la población, de modo que la diferencia entre el valor encontrado y el valor real sea lo más pequeña posible. Y ahí es donde nace la idea del error de muestreo.

Las muestras se utilizan para estimar las características de toda la población. La diferencia entre el valor obtenido con la muestra y el valor real obtenido con toda la población se denomina error de muestreo. Es imposible saber exactamente cuánto vale el error de muestreo, dado que se desconoce el valor real (¡recuerde que esto es exactamente lo que motivó el uso de una muestra!). Sin embargo, es posible obtener información importante sobre el tamaño del error de muestreo utilizando técnicas estadísticas.

En este artículo, describiremos cómo se puede calcular el tamaño ideal de la muestra, en función del tamaño de la población total y del margen de error tolerable, concepto que explicaremos más adelante. Se presentarán algunas fórmulas simplificadas a título ilustrativo. Sin embargo, antes de eso, es importante explorar algunos conceptos relevantes como el margen de error y el intervalo de confianza.

Error de muestreo e intervalo de confianza

El margen de error es un indicador relacionado con la cantidad de error de muestreo en los resultados de una encuesta. Además del margen de error, los resultados de una encuesta también se asocian a un intervalo de confianza.  

Es muy común ver el siguiente tipo de comentarios en época de elecciones: “el candidato A obtuvo un 65% de intención de voto, con un margen de error de más o menos 2%. El intervalo de confianza de la encuesta es del 95%”. Pero, ¿qué significa realmente todo esto?

Si el 65% de los encuestados dijo que tenía la intención de votar por el candidato A, pero el margen de error es del 2% más o menos, hay que considerar que el porcentaje real de intenciones probablemente debería estar entre el 63% y el 67%.

Sin embargo, esto no significa que el valor real esté necesariamente dentro de este rango. Hay un intervalo de confianza asociado. ¿Qué significa que el intervalo de confianza es del 95%?

Es muy importante entender el concepto de intervalo de confianza, ya que muchas personas tienen una interpretación falsa sobre él. Es común tener la idea errónea de que habrá un 95% de posibilidades de que el valor real esté entre el 63% y el 67%.

En realidad, un intervalo de confianza del 95% significa que si la encuesta se repite varias veces, tomando muestras diferentes, en el 95% de los casos el valor verdadero estará contenido dentro del rango obtenido con el margen de error.

Pongamos un mejor ejemplo: con la muestra considerada anteriormente, el candidato A obtuvo un 65% de intención de voto, y como el margen de error es de más o menos 2%, el rango en el que posiblemente el valor real debería estar entre el 63% y el 67%. Eligiendo otra muestra de la misma población, y realizando de nuevo la encuesta, es posible que el valor dé un 64%, y como el margen de error es del 2%, el rango sería del 62% al 66%. El intervalo de confianza del 95% significa que cuando la encuesta se repite muchas veces con muchas muestras diferentes, el 95% de las veces el valor verdadero estará dentro del margen de error y el 5% de las veces, estará fuera.

También existe la idea errónea de que si el intervalo de confianza es del 95%, repitiendo la encuesta muchas veces, se obtendrá el mismo resultado el 95% de las veces. De acuerdo con lo visto anteriormente, esta interpretación representa un grave error en la comprensión del concepto.

Cómo establecer el tamaño de una muestra

Como se mencionó anteriormente, el tamaño de una muestra depende del tamaño de la población y del margen de error tolerable. De la teoría matemática de la estadística, tenemos la siguiente expresión:

En la expresión anterior:

n: tamaño de la muestra a calcular;

N: tamaño de la población;

Z: nivel de confianza elegido, expresado como número de desviaciones típicas;

P: Es la proporción que se espera encontrar;

y: margen de error máximo tolerado.

La variable p puede causar cierta extrañeza a primera vista, ya que este es precisamente el valor que se está calculando en la investigación. La razón por la que existe este parámetro es porque cuando se tiene una noción previa de investigaciones previas (por ejemplo, sabiendo que la proporción suele estar entre el 10% y el 20%) es posible elegir muestras más pequeñas, porque ya se tiene cierta información relevante.

Cuando no tienes idea de qué esperar, lo mejor que puedes hacer es elegir p = 0,5, lo que significa asumir el peor de los casos: la población está dividida en partes iguales. Por lo tanto, la regla general es usar p = 50%.

Para los valores más típicos del intervalo de confianza, existen valores ya calculados y tabulados para Z. Para el caso del intervalo de confianza del 95%, se obtiene Z=1,96.

A continuación se presenta una fórmula simplificada (obtenida considerando que el primer término del denominador es mucho mayor que el segundo y luego teniendo en cuenta que, dado que N es muy grande, entonces N≈N-1) que relaciona el tamaño de la muestra y el error de muestreo:

Adoptando p=50%:

Como se ve, en muchos casos, Z=1,96. Considerando que 1.962≈4 y sustituyendo en la ecuación anterior, obtenemos la siguiente fórmula, aún más simplificada:

La aproximación anterior es razonable solo para el nivel de confianza del 95% y muestra una forma bastante rápida de calcular el tamaño aproximado de una muestra conociendo el error de muestreo, y viceversa.

Además de la extrema simplicidad de esta fórmula, también es interesante notar que ya no depende del tamaño total de la población N – es importante recordar que esto sucedió después de que se hizo la simplificación de considerar que N era muy grande, típicamente mayor que 10 mil.

Por lo tanto, la fórmula simplificada debería aportar buenas aproximaciones en muchos casos, sin embargo, no debería utilizarse en casos de poblaciones pequeñas.

A modo de ilustración, considere un caso en el que desea obtener un error de muestreo muy bajo del 2%. En este caso, utilizando la fórmula más simplificada que obtuvimos, deberíamos utilizar una muestra de aproximadamente  = 2.500 personas.

Por otro lado, cuando se tiene una muestra de 12 mil personas, el margen de error será aproximadamente   = 0.91%.

Cómo utilizar estos conceptos a tu favor

Las encuestas de satisfacción con muchos elementos a evaluar a menudo son ignoradas o abandonadas por los clientes. Se vuelve agotador para alguien, en el ajetreo de la vida cotidiana, tener que detenerse y reflexionar para evaluar numerosos ítems, tales como: Servicio, Precio, Calidad del Producto, Entorno de la Tienda, Variedad, Tiempo de Espera, etcétera. Pero, ¿es realmente necesario pedir a todos los clientes que califiquen todos los artículos?

Una forma más inteligente de obtener comentarios de los clientes sobre aspectos de un negocio sería hacer una cantidad menor de preguntas para cada cliente, haciendo que diferentes clientes respondan diferentes conjuntos de preguntas.

La idea detrás de esto es: no es necesario que todos los clientes respondan a cada artículo. Para cada ítem, solo es necesario tener una muestra suficiente de respuestas para obtener un margen de error bajo.

Especificando que se desea un margen de error del 2% en el ítem de Servicio al Cliente, por ejemplo, basta con que aproximadamente 2.500 personas respondan a esta pregunta, y no toda la población, como se ve en los párrafos anteriores.

Esto permite obtener resultados fiables sin tener que someter a los clientes a una larga y agotadora investigación.

Acerca de SoluCX

SoluCX es una startup nacida en São José dos Campos  (SP) que ofrece soluciones para la gestión de la experiencia del cliente
cliente (CX).
Con su metodología innovadora, las empresas de todos los tamaños tienen acceso a información fundamental para entender el comportamiento de los clientes y su relación con la marca, lo que les permite delinear estrategias para generar mejores resultados financieros a partir de la fidelización y mejora de servicios y procesos, creando una relación más cercana con las comunidades donde operan.