Assim como em pesquisas eleitorais, a maior parte das pesquisas quantitativas utilizam a fórmula de erro amostral para determinar seu nível de precisão.
A teoria para essa metodologia é explicada neste artigo.
No entanto, assim como exemplificado no texto do link acima, essa fórmula funciona para avaliar resultados concorrentes, ou seja, em uma pesquisa eleitoral, você irá avaliar as chances de vitória entre os candidatos A, B, C e D.

Para pesquisas de satisfação como CSAT, CES, Likes e Dislikes entre outras com múltipla escolha, essa metodologia funciona e é a mais adequada.
Por que esse método não serve para o NPS?
Fazendo um paralelo com a pesquisa eleitoral, vamos supor que o Promotor é um candidato e o Detrator é o outro.
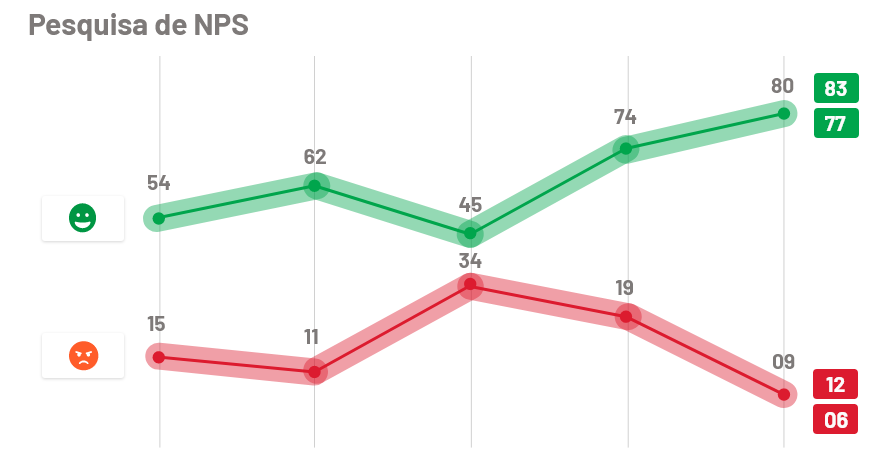
Diferente das pesquisas de múltipla escolha com leitura direta descritas acima (CSAT, CES, Likes & Dislikes entre outras de múltipla escolha), o NPS (Net Promoter Score) é composto por uma subtração entre os tipos de clientes (Promotores e Detratores).:
NPS = % Promotores – % Detratores
Sendo assim, ao subtrair os Detratores dos Promotores, cada um com margem de erro de ±3%, estaríamos somando o erro das duas categorias de clientes e obtendo ±6% de erro amostral.
E então? Qual a melhor maneira para o NPS?
Primeiro deve-se calcular o Standard Error (SE) ou Erro padrão, como mostrado a seguir:

Logo depois se obtêm o intervalo de confiança ou Margem de erro, da seguinte maneira:
NPS ± 1,96 * SE
Sendo 1,96 o valor referente a um nível de confiança de 95%.
Para facilitar o entendimento exemplificamos para você:
Vamos supor que você fez uma pesquisa que recebeu 10.000 respostas, na qual 6000 (60%) eram promotores, 2000 (20%) eram neutros e 2000 (20%) eram detratores e deseja calcular o erro do NPS.
NPS = 60 – 20 = 40
Primeiro Passo: Seguindo nosso exemplo acima, vamos calcular o Standard Error (SE), isto é, o Erro Padrão da pesquisa. Obtendo os seguintes valores:
Promotor = 0,6
Neutro = 0,2
Detrator = 0,2
Avaliações Respondidas = 10.000
Erro Padrão (SE) = 0,8%
Segundo Passo: Sabendo o Erro Padrão, identificado no primeiro passo, vamos determinar o intervalo de confiança (Margem de Erro) do NPS, considerando uma confiabilidade de 95%:
Margem de Erro: 1,96 * 0,8 = 1,6
Voltando ao nosso exemplo, o intervalo de confiança do NPS passaria a ser:
NPS = 40 com margem de erro de ± 1,6
Ou seja, ao realizar a pesquisa com diferentes amostras de seus clientes, o seu NPS estará entre 38,4 e 41,6 em 95% das vezes.
Mas e se eu quiser melhorar minha margem de erro no NPS? Como faço? Preciso de muitas avaliações?
Preparamos para você um resumo para não se preocupar mais com isso! Confira abaixo a quantidade de respostas que você precisa para ter a margem de erro desejada no seu NPS!
| Margem de Erro | Quantidade de Respostas |
| ± 10% | 385 |
| ± 5% | 1.600 |
| ± 1% | 40.000 |
| ± 0,5% | 154.000 |
Como nosso objetivo com esse texto é reduzir o seu esforço, disponibilizamos essa Calculadora de Erro Amostral e Tamanho de Amostra para pesquisas de satisfação, onde você pode aplicar à cada uma das metodologias.
Viu como é fácil? Caso tenha alguma dúvida em alguns dos passos ou queira se aprofundar mais na teoria, disponibilizamos o estudo completo sobre o Erro Amostral aplicado ao NPS.
Quer ter acesso a mais conteúdos? Acesse nossa Biblioteca de CX.





