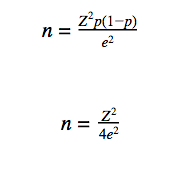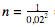Entenda neste post tudo que você precisa sobre erro amostral e tamanho de amostra. Aprenda a utilizar estes conceitos a seu favor para otimizar suas pesquisas e obter os melhores resultados utilizando poucos recursos. Veja abaixo:

por Fernando Saraiva

Em uma eleição de um país, quantas pessoas precisam ser entrevistadas para se descobrir as porcentagens exatas de indivíduos que têm intenção de votar em cada candidato? Se o objetivo é realmente descobrir a informação de maneira totalmente exata, a resposta é simples: é necessário entrevistar todas as pessoas do país.

Entretanto, em um país de dimensões continentais, como o Brasil, entrevistar todas as pessoas é algo completamente inviável. As quantidades de tempo e de dinheiro gastas em uma pesquisa como essa seriam absurdamente grandes. Porém, é realmente necessário saber as porcentagens exatas das intenções de votos de cada candidato? Qual é a real necessidade? Será que resultados aproximados não seriam suficientes?

A verdade é que, especialmente em pesquisas relacionadas a populações muito grandes, não se analisa a população inteira, mas apenas uma parcela dela, chamada de amostra. Essa amostra é escolhida com um tamanho suficiente para que o comportamento dela possa ser uma boa aproximação ou estimativa para o comportamento da população inteira, isto é, a amostra precisa ser representativa da população.

Obviamente, quando se analisa apenas uma parcela da população, e não ela inteira, são obtidos resultados diferentes, devido ao fato de que uma parte da informação total foi perdida, já que a amostra não contém todos os elementos da população. O objetivo é escolher uma amostra que represente bem a população, de forma que a diferença entre o valor encontrado e o valor verdadeiro seja a menor possível. E é aí que nasce a ideia de erro amostral.

As amostras são usadas para estimar características da população inteira. A diferença entre o valor obtido com a amostra e o valor verdadeiro obtido com a população toda é chamada de erro amostral. É impossível saber exatamente quanto vale o erro amostral, dado que o valor verdadeiro é desconhecido (lembre-se que foi exatamente isso que motivou o uso de uma amostra!). Porém, é possível obter importantes informações sobre o tamanho do erro amostral utilizando técnicas estatísticas.

Neste artigo, descreveremos como se pode calcular o tamanho ideal de uma amostra, dependendo do tamanho da população total e da margem de erro tolerável, conceito que vamos explicar adiante. Algumas fórmulas simplificadas serão apresentadas para ilustração. Porém, antes disso, é importante explorar alguns conceitos relevantes como margem de erro e intervalo de confiança.

Erro amostral e Intervalo de Confiança

A margem de erro é um indicador relacionado à quantidade de erro amostral nos resultados de uma pesquisa. Além da margem de erro, os resultados de uma pesquisa também estão associados a um intervalo de confiança.  

É muito comum ver o seguinte tipo de comentário em época de eleições: “o candidato A obteve 65% de intenção de voto, com margem de erro de 2% para mais ou para menos. O intervalo de confiança da pesquisa é de 95%”. Mas o que isso tudo significa realmente?

Se 65% dos entrevistados disseram que tinham intenção de votar no candidato A, mas a margem de erro é de 2% para ou mais ou para menos, devemos considerar que a porcentagem real de intenções deve provavelmente ficar entre 63% e 67%.

Porém, isso não significa que obrigatoriamente o valor verdadeiro está dentro desse intervalo. Há um intervalo de confiança associado. O que significa o fato de o intervalo de confiança ser de 95%?

É bastante importante entender o conceito de intervalo de confiança, pois muitas pessoas possuem uma interpretação falsa sobre ele. É comum a ideia errônea de que existirá 95% de chance de o valor verdadeiro estar entre 63% e 67%.

Na realidade, um intervalo de confiança de 95% significa que, se a pesquisa for repetida várias vezes, tomando diferentes amostras, em 95% dos casos o valor verdadeiro estará contido dentro do intervalo obtido com a margem de erro.

Vamos exemplificar melhor: com a amostra considerada anteriormente, o candidato A obteve 65% de intenção de voto, e como a margem de erro é de 2% para mais ou para menos, o intervalo em que o valor real possivelmente deve estar é entre 63% e 67%. Escolhendo outra amostra da mesma população, e realizando a pesquisa novamente, é possível que o valor dê 64%, e como a margem de erro é de 2%, o intervalo seria de 62% a 66%. O intervalo de confiança de 95% significa que, quando se repete a pesquisa muitas vezes com muitas amostras diferentes, em 95% das vezes o valor verdadeiro estará dentro do intervalo da margem de erro, e em 5% das vezes, ele estará fora.

Existe também a noção errada de que se o intervalo de confiança é de 95%, repetindo a pesquisa muitas vezes, será obtido o mesmo resultado 95% das vezes. De acordo com o que vimos anteriormente, essa interpretação representa um erro grave no entendimento do conceito.

Como definir o tamanho de uma amostra

Como já mencionado anteriormente, o tamanho de uma amostra depende do tamanho da população e da margem de erro tolerável. Da teoria matemática da estatística, tem-se a seguinte expressão:

Na expressão acima:

n: tamanho da amostra que se quer calcular;

N: tamanho da população;

Z: nível de confiança escolhido, expresso em número de desvios padrão;

p: é a proporção que se espera encontrar;

e: margem de erro máxima tolerada.

A variável p pode causar certa estranheza à primeira vista, pois esse é justamente o valor que se está tentando calcular na pesquisa. A razão pela qual esse parâmetro existe é porque quando se tem uma noção prévia vindo de pesquisas anteriores (por exemplo, saber que a proporção costuma estar entre 10% e 20%) é possível escolher amostras menores, pois já se possui alguma informação relevante.

Quando não se possui nenhuma ideia sobre o que se deve esperar, o melhor a se fazer é escolher p=0,5, que significa assumir o pior cenário: a população se divide em partes iguais. Assim, a regra geral é usar p=50%.

Para os valores mais típicos de intervalo de confiança, há valores já calculados e tabelados para Z. Para o caso do intervalo de confiança de 95%, tem-se Z=1,96.

Uma fórmula simplificada (obtida considerando que o primeiro termo do denominador é bem maior que o segundo e depois levando em conta que, como N é muito grande, então N≈N-1) que relaciona o tamanho da amostra e o erro amostral é dada a seguir:

Adotando p=50%:

Como visto, em muitos casos, Z=1,96. Considerando que 1,962≈4 e substituindo na equação anterior, obtém-se a fórmula a seguir, ainda mais simplificada:

A aproximação anterior é razoável apenas para o nível de confiança de 95% e mostra uma maneira bastante rápida de calcular o tamanho aproximado de uma amostra conhecendo o erro amostral, e vice-versa.

Além da extrema simplicidade dessa fórmula, é interessante notar também que ela não depende mais do tamanho total da população N – é importante lembrar que isso aconteceu depois que foi feita a simplificação de considerar que N era muito grande, tipicamente maior que 10 mil.

Portanto, a fórmula simplificada deve trazer boas aproximações em muitos casos, entretanto não deve ser utilizada em casos de populações pequenas.

Para efeito de ilustração, considere um caso em que se deseja obter um erro amostral bem baixo, de 2%. Nesse caso, utilizando a fórmula mais simplificada que obtivemos, deve-se utilizar uma amostra de aproximadamente  = 2.500 pessoas.

Por outro lado, quando se possui uma amostra de 12 mil pessoas, a margem de erro será de aproximadamente  =0,91%.

Como utilizar esses conceitos a seu favor

Pesquisas de satisfação com muitos itens a serem avaliados costumam ser frequentemente ignoradas ou abandonadas pelos clientes. Torna-se desgastante para alguém, na correria do cotidiano, ter que parar e refletir para avaliar numerosos itens, tais como: Atendimento, Preço, Qualidade do Produto, Ambiente da loja, Variedade, Tempo de Espera, etc. Mas será que é mesmo necessário pedir para que todos os clientes avaliem todos os itens?

Uma maneira mais inteligente de obter feedback dos clientes sobre os aspectos de uma empresa seria fazer uma quantidade menor de perguntas para cada cliente, fazendo com que diferentes clientes respondam a diferentes conjuntos de perguntas.

A ideia por trás disso é: não é necessário que todos os clientes respondam a todos os itens. Para cada item, só é necessário ter uma amostra de respostas suficiente para obter uma margem de erro baixa.

Especificando que se deseja uma margem de erro de 2% no quesito Atendimento ao Cliente, por exemplo, basta que aproximadamente 2.500 pessoas respondam a esse quesito, e não a população inteira, como visto nos parágrafos anteriores.

Isso possibilita a obtenção de resultados confiáveis sem precisar submeter os clientes a longas e desgastantes pesquisas.

Sobre a SoluCX

A SoluCX é uma startup nascida em São José dos Campos (SP) que oferece soluções para gestão da experiência do
cliente (CX).
Com sua metodologia inovadora, empresas de todos os portes têm acesso a informações fundamentais para entender o comportamento do cliente e sua relação com a marca, o que permite traçar estratégias para gerar melhores resultados financeiros a partir da fidelização e aprimoramento de serviços e processos, criando uma relação mais próxima com as comunidades onde estão inseridas.