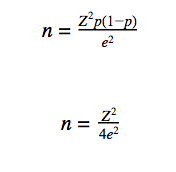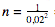Understand in this post everything you need about sampling error and sample size. Learn how to use these concepts to your advantage to optimize your searches and get the best results using few resources. See below:

by Fernando Saraiva

In a country’s election, how many people need to be interviewed to find out the exact percentages of individuals who intend to vote for each candidate? If the goal is really to find out the information in a completely accurate way, the answer is simple: it is necessary to interview all the people in the country.

However, in a country of continental dimensions, such as Brazil, interviewing all people is completely unfeasible. The amounts of time and money spent on research like this would be absurdly large. However, is it really necessary to know the exact percentages of each candidate’s voting intentions? What is the real need? Wouldn’t approximate results be enough?

The truth is that, especially in research related to very large populations, the entire population is not analyzed, but only a portion of it, called a sample. This sample is chosen with a sufficient size so that its behavior can be a good approximation or estimate for the behavior of the entire population, that is, the sample needs to be representative of the population.

Obviously, when only a portion of the population is analyzed, and not the entire one, different results are obtained, due to the fact that a part of the total information was lost, since the sample does not contain all the elements of the population. The objective is to choose a sample that represents the population well, so that the difference between the value found and the true value is as small as possible. And that’s where the idea of sampling error is born.

The samples are used to estimate characteristics of the entire population. The difference between the value obtained with the sample and the true value obtained with the entire population is called sampling error. It’s impossible to know exactly how much the sampling error is worth, given that the true value is unknown (remember that this is exactly what motivated the use of a sample!). However, it is possible to obtain important information about the size of the sampling error using statistical techniques.

In this article, we will describe how the ideal sample size can be calculated, depending on the size of the total population and the tolerable margin of error, a concept that we will explain later. Some simplified formulas will be presented for illustration. However, before that, it is important to explore some relevant concepts such as margin of error and confidence interval.

Sampling Error and Confidence Interval

The margin of error is an indicator related to the amount of sampling error in the results of a survey. In addition to the margin of error, the results of a survey are also associated with a confidence interval.  

It is very common to see the following type of comment at election time: “candidate A obtained 65% of voting intention, with a margin of error of plus or minus 2%. The confidence interval of the survey is 95%”. But what does it all really mean?

If 65% of respondents said they intended to vote for candidate A, but the margin of error is 2% plus or minus, we must consider that the actual percentage of intentions should probably be between 63% and 67%.

However, this does not mean that the true value is necessarily within this range. There is an associated confidence interval. What does it mean that the confidence interval is 95%?

It is very important to understand the concept of confidence interval, as many people have a false interpretation about it. It is common to have the erroneous idea that there will be a 95% chance that the true value is between 63% and 67%.

In reality, a 95% confidence interval means that if the survey is repeated several times, taking different samples, in 95% of cases the true value will be contained within the range obtained with the margin of error.

Let’s give a better example: with the sample considered above, candidate A obtained 65% of voting intention, and as the margin of error is plus or minus 2%, the range in which the real value should possibly be between 63% and 67%. Choosing another sample from the same population, and conducting the survey again, it is possible that the value gives 64%, and as the margin of error is 2%, the range would be 62% to 66%. The 95% confidence interval means that when the survey is repeated many times with many different samples, 95% of the time the true value will be within the margin of error, and 5% of the time, it will be outside.

There is also the misconception that if the confidence interval is 95%, repeating the survey many times, the same result will be obtained 95% of the time. According to what we have seen earlier, this interpretation represents a serious error in the understanding of the concept.

How to set a sample size

As mentioned earlier, the size of a sample depends on the size of the population and the tolerable margin of error. From the mathematical theory of statistics, we have the following expression:

In the expression above:

n: size of the sample to be calculated;

N: population size;

Z: chosen confidence level, expressed as number of standard deviations;

p: it is the proportion that is expected to be found;

and: maximum tolerated margin of error.

The variable p may cause some strangeness at first glance, as this is precisely the value that is being calculated in the research. The reason why this parameter exists is because when you have a prior notion from previous research (for example, knowing that the proportion is usually between 10% and 20%) it is possible to choose smaller samples, because you already have some relevant information.

When you have no idea what to expect, the best thing to do is to choose p=0.5, which means assuming the worst-case scenario: the population is divided into equal parts. Thus, the general rule of thumb is to use p=50%.

For the most typical values of the confidence interval, there are values already calculated and tabulated for Z. For the case of the 95% confidence interval, Z=1.96 is obtained.

A simplified formula (obtained by considering that the first term of the denominator is much larger than the second and then taking into account that, since N is very large, then N≈N-1) that relates the sample size and the sampling error is given below:

Adopting p=50%:

As seen, in many cases, Z=1.96. Considering that 1.962≈4 and substituting in the previous equation, we obtain the following formula, even more simplified:

The previous approximation is reasonable only for the 95% confidence level and shows a fairly quick way to calculate the approximate size of a sample knowing the sampling error, and vice versa.

In addition to the extreme simplicity of this formula, it is also interesting to note that it no longer depends on the total size of the population N – it is important to remember that this happened after the simplification of considering that N was very large, typically larger than 10 thousand, was made.

Therefore, the simplified formula should bring good approximations in many cases, however it should not be used in cases of small populations.

For the sake of illustration, consider a case in which you want to obtain a very low sampling error of 2%. In this case, using the most simplified formula we obtained, we should use a sample of approximately  = 2,500 people.

On the other hand, when you have a sample of 12 thousand people, the margin of error will be approximately   = 0.91%.

How to use these concepts to your advantage

Satisfaction surveys with many items to be evaluated are often ignored or abandoned by customers. It becomes exhausting for someone, in the rush of everyday life, to have to stop and reflect to evaluate numerous items, such as: Service, Price, Product Quality, Store Environment, Variety, Waiting Time, etc. But is it really necessary to ask all customers to rate all items?

A smarter way to get feedback from customers about aspects of a business would be to ask a smaller amount of questions for each customer, having different customers answer different sets of questions.

The idea behind this is: it is not necessary for all customers to respond to every item. For each item, it is only necessary to have a sufficient sample of responses to obtain a low margin of error.

Specifying that a margin of error of 2% is desired in the Customer Service item, for example, it is enough for approximately 2,500 people to respond to this question, and not the entire population, as seen in the previous paragraphs.

This makes it possible to obtain reliable results without having to subject customers to long and exhausting research.

About SoluCX

SoluCX is a startup born in São José dos Campos  (SP) that offers solutions for managing the customer experience
customer (CX).
With its innovative methodology, companies of all sizes have access to fundamental information to understand customer behavior and their relationship with the brand, which allows them to outline strategies to generate better financial results from loyalty and improvement of services and processes, creating a closer relationship with the communities where they operate.